[勉強ノート] 「線形計算の数理」 7.7.1 Arnoldi法
前回に引き続き線形計算の数理の固有値問題で紹介されていたアルゴリズムについての解説になります。今日はその中のArnoldi法についての説明です。
このArnoldi法をはじめとしたRayleigh-Ritzの技法ベースの手法は個人的には初見で「どれもアルゴリズムはわかるけど、なんでそれでうまくいくのさっぱり」という感じだったので、本の解説の中で自分のわからなかった部分を補足しながら説明をしていければと思います。
Pythonの実装はこちらにあります。
https://github.com/shu65/theoretical-numerical-linear-algebra/blob/main/%E7%B7%9A%E5%BD%A2%E8%A8%88%E7%AE%97%E3%81%AE%E6%95%B0%E7%90%86_7_7_1_Arnoldi%E6%B3%95.ipynb
目次
Arnoldi法とは
ある次元の不変部分空間\(E\)の近似空間\(F\)が与えられたとき、\(E\)に対応する固有値と固有ベクトルの近似値を近似空間\(F\)を使って求めるRayleigh-Ritzの技法というものがあります。
このRayleigh-Ritzの技法ベースの手法の一つで、Krylov部分空間と呼ばれる空間で近似空間を作る手法がArnoldi法です。大規模な行列の際、QR法などの固有値、固有ベクトルを求めるアルゴリズムを直接適用すると計算量や必要なメモリサイズの観点で適用が難しい場合があります。このような場合にArnoldi法は利用されます。
Arnoldi法のアルゴリズムやRayleigh-Ritzの技法、Krylov部分空間についてはこの後より詳しく説明していきます。
Arnoldi法のアルゴリズム
まずはArnoldi法のアルゴリズム説明します。本ではアルゴリズム全体についてちゃんと書かれておらず、いろいろなサイトを調べましたが、ちょっとずつ違うので、今回は近似固有値、近似固有ベクトルまで求めるシンプルなものを説明します。
Arnoldi法は入力として以下のものを取ります。
- \( A\): 固有値、固有ベクトルを計算する複素\( n \)次正方行列
- \(\boldsymbol{x}_0\): \(\boldsymbol{x}_0 \ne 0\)の\( n \)次元ベクトル
- \(m\): 生成する部分空間の次元数。\(m \le n\)
これらを入力として以下のように計算していきます。
- \( A \) と \(\boldsymbol{x}_0\)を入力に取る。
- \(H\)をすべての要素が0の行列として初期化する。
- \(\boldsymbol{v}_0 := \boldsymbol{x}_0/||\boldsymbol{x}_0|| \)
- \(k\)を\(0\) から \(m-1\)まで以下を繰り返す。
- \(\boldsymbol{w} := A\boldsymbol{v}_k\)
- \(i\)を\(0\) から \(k\)まで以下を繰り返す。
- \(H_{i,k} := \boldsymbol{v}_i^H \boldsymbol{w}\)
- \(\boldsymbol{w} := \boldsymbol{w} – H_{i,k} \boldsymbol{v}_i\)
- \(H_{k+1,k} := || \boldsymbol{w} ||\)
- \(\boldsymbol{v}_{k+1} := \boldsymbol{w} / H_{k+1,k}\)
- \(H\)の固有値と固有ベクトルを求め、それぞれをRitz値(\(\theta_0, …, \theta_m\))とRitzベクトル(\( \boldsymbol{y}_0, …, \boldsymbol{y}_m\))とする
- \( V = [\boldsymbol{v_0}, …, \boldsymbol{v}_m]\) とし、以下の計算を(k)が(0) から (m)まで繰り返す。
- \(\boldsymbol{z}_k = \boldsymbol{V}y_k\)
- Ritz値(\(\theta_0, …, \theta_m\))を\(A\)の固有値の近似値、\(\boldsymbol{z}_k\)を\(A\)の固有値の近似固有ベクトルとして出力する
1-4は正規直交基底を生成しつつ、\(H\)を作っているためわかりにくいですが、正規直交基底を作っている部分は\( \boldsymbol{x}_0, A\boldsymbol{x}_0, A^2\boldsymbol{x}_0, …, A^{m-1}\boldsymbol{x}_0\) に対してグラムシュミットの正規直交化法を適用しているだけです。
なので、アルゴリズム自体は難しいものではないと思っています。
ちなみにこのアルゴリズムで\(H\)は対角成分の一つ下の要素も値が埋まっている上三角行列であるHessenberg行列になります。この際、アルゴリズムの4.3.行目が対角成分の一つ下の要素を代入しているところになります。ここで、この4.3.行目で代入する値は、ここまで生成した正規直交基底\(\boldsymbol{v}_0, …, \boldsymbol{v}_k\)で\(A^k\boldsymbol{x}_0\)を表しきれなかったベクトルのノルムを代入していると見ることができます。実はこのノルムが0に近ければ、ここまでで生成した正規直交基底\(\boldsymbol{v}_0, …, \boldsymbol{v}_k\)で\(A^k\boldsymbol{x}_0\)を表現できるとみることができ、これ以降のKrylov列の要素も表現できます。このため、アルゴリズムのバリエーションとしては4.3.行目のノルムの値をチェックして、0に近ければそこで正規直交基底の生成をストップするというものもあります。
このアルゴリズムにおいて\(m\)は何個の固有値、固有ベクトルを求めるかや近似精度をどこまで上げるか?など重要なものを決定づけています。ただ、実際にArnoldi法でいろいろ実験をしてみればわかりますが、\(m\)を事前に決めておくのは難しく、実用を考えると後ほど紹介する残差ベクトルを使って、近似空間を拡大するかどうか判断するようなアルゴリズムのほうが使い勝手は良いかと思います。
ちなみに1-4までの処理を指してArnoldi法と言っているサイトや講義資料もありました。なので、一体どこからどこまでの処理がArnoldi法かはわからないですが、今回は固有値を求めるところまでをArnoldi法と呼びます。
Arnoldi法によってなぜ固有値、固有ベクトルの近似値が求まるのか?
先ほど説明した通り、Arnoldi法のアルゴリズム自体は難しいことをしてないのですが、それがなぜうまくいくのかは本を読んでもわからないことが多かったので詳しく説明していきます。
Rayleigh-Ritzの技法 / 射影法
Arnoldi法がなぜうまくいくかを説明するために、Rayleigh-Ritzの技法(または射影法と呼ぶ場合もあります)をまずは説明していきます。
Rayleigh-Ritzの技法は不変部分空間\(E\)の近似空間\(F\)が与えられたとき、\(E\)に対する固有値、固有ベクトルの近似値を\(F\)を使って求める手法全般を指します。
もう少し具体的に説明していきます。ある\(m\)次元不変部分空間\(E\)を\(A\)の\(m\)本の固有ベクトル \(\boldsymbol{z}_{i_1}, … ,\boldsymbol{z}_{i_m}\)で張られた空間であるとします。ここでポイントですが、\(E\)は\(A\)のすべての固有ベクトルで張られた空間である必要はなく、一部の固有ベクトルだけで張られた空間であることを注意してください。また、\(\boldsymbol{z}_{i_1}, …, \boldsymbol{z}_{i_m}\)に対応する\(A\)の固有値を\(\lambda_{i_1}, … \lambda_{i_m}\)とします。このとき、固有値、固有ベクトルの性質から以下の関係が成り立ちます。
$$ \begin{align*}
AZ_m = Z_m\Lambda_m \tag{7.42.1}
\end{align*} $$
ただし、\(Z_m = [\boldsymbol{z}_{i_1}, … \boldsymbol{z}_{i_m}]\)、\(\Lambda_m = \text{diag}(\lambda_{i_1}, … \lambda_{i_m})\)です。
次に\(E\)の任意の正規直交基底\( \boldsymbol{u}_1, … , \boldsymbol{u}_m\)をとって、\(U=[\boldsymbol{u}_{1}, … \boldsymbol{u}_{m}]\)とします。\( \boldsymbol{u}_1, … , \boldsymbol{u}_m\)はAの固有ベクトルとは別もので大丈夫です。\(U\)は正規直交基底なので以下が成り立ちます。
$$ \begin{align*}
U^HU = I_m \tag{7.42.2}
\end{align*} $$
この\(U\)を使うと\(Z_m\)はある\(m\)次行列\(Y\)を使って以下のように書けます。
$$ \begin{align*}
Z_m = UY \tag{7.42.3}
\end{align*} $$
これは単純に\(Z_m\)を\(\boldsymbol{u}_{1}, … \boldsymbol{u}_{m}\)を使って表すことができることを指しています。
そして、式(7.42.1)の左から\(U^H\)を掛け、式(7.42.2)、(7.42.3)を使って変形すると以下のようになります。
$$ \begin{align*}
U^HAZ_m =& U^HZ_m\Lambda_m \\
U^HAUY =& U^HUY\Lambda_m \\
U^HAUY =& I_mY\Lambda_m \\
U^HAUY =& Y\Lambda_m
\tag{7.42}
\end{align*} $$
ここで分かりやすいように\(U^HAU=B\)と置くと以下のようになります。
$$ \begin{align*}
BY =& Y\Lambda_m
\tag{7.42.4}
\end{align*} $$
これは\(m\)次行列\(B\)に対する固有値問題の形になっています(\(Y\)の列ベクトルが固有ベクトル、\(\Lambda_m\)の対角成分が固有値)。ここで\(m \le n\)であることを思い出すと、\(A\)よりも小さい行列\(B\)の固有値を求めれば\(A\)の固有値の一部がわかることを示しています。また、\(A\)の固有ベクトルに関しても、式(7.42.3)から簡単に求めることができます。
ここまでは不変部分空間\(E\)を使っていましたが、実際には\(E\)は未知です。なので、\(E\)を近似する部分空間\(F\)を適当に選ぶことにします。\(F\)の正規直交基底\(\boldsymbol{v}_{1}, … \boldsymbol{v}_{m}\)を並べた行列\(V=[\boldsymbol{v}_{1}, … \boldsymbol{v}_{m}]\)とします。この\(V\)を使って式(7.42)の\(U\)を\(V\)に置き換えたような以下の式を考えます。
$$ \begin{align*}
V^HAV\boldsymbol{y} =& \theta\boldsymbol{y}
\tag{7.42}
\end{align*} $$
これは\(m\)次行列\(V^HAV\)の固有値問題になっています。この\(V^HAV\)の固有値問題を何等かの方法(QR法など)で解き、\(\theta\)を\(A\)の固有値の近似値、\(\boldsymbol{z} = V\boldsymbol{y}\)を\(A\)の固有ベクトルの近似とします。
これをRayleigh-Ritzの技法といい、近似固有値\(\theta\)はRitz値、近似固有ベクトル\(\boldsymbol{z}\)をRitzベクトルといいます。
通常は\(m\)を事前に決めておくのではなく、以下の残差ベクトル\(\boldsymbol{r}\)を導入して近似部分空間\(F\)を拡大するかどうかを判断します。
$$ \begin{align*}
\boldsymbol{r} =& A\boldsymbol{z} – \theta\boldsymbol{z}
\tag{7.43.1}
\end{align*} $$
\(\theta\)と\(\boldsymbol{z}\)がAの固有値、固有ベクトルに十分近ければ\(r\)は十分小さくなります。このため、\(r\)が十分小さければ\(\theta\)と\(\boldsymbol{z}\)を採用し、\(r\)が大きいときは近似部分空間\(F\)を拡大します。
ちなみにRayleigh-Ritzの技法は近似部分空間をどういう風に作るかは特に言及されていません。ただ、このRayleigh-Ritzの技法ではどういう部分空間を作るかによって、\(A\)の固有値のどの部分の固有値を近似するのか(絶対値が最大となる固有値など)や近似精度などが決定いします。このため、この近似部分空間をどう作るかは重要なポイントになります。
Arnoldi法はこの近似部分空間としてKrylov部分空間を利用している手法になります。また、Arnoldi法以外のRayleigh-Ritzの技法ベースの手法としては以下のものがあります。
- Lanczos法: エルミート行列に対するArnoldi法
- Jacobi-Davidson法: Krylov部分空間を使わずに部分空間の列を構成する手法
Krylov部分空間
ここではArnoldi法で利用されているKrylov部分空間について説明します。
ベクトル\(\boldsymbol{x}\)に行列\(A\)のべき乗掛けて生成される列 \( \boldsymbol{x}, A\boldsymbol{x}, A^2\boldsymbol{x},…\) (Krylov列と言います)の最初の\(k\)個のベクトルの張る部分空間
$$ \begin{align*}
\mathcal{K}_k(A, \boldsymbol{x}) = \text{span}(\boldsymbol{x}, A\boldsymbol{x}, A^2\boldsymbol{x}, …, A^{k-1}\boldsymbol{x})
\tag{4.94}
\end{align*} $$
を\(k\)次のKrylov部分空間と呼びます。
Krylov部分空間の特徴として本で紹介されていることとしてはKrylov部分空間は\(\boldsymbol{x}\)を含む最小の\(A\)不変部分空間に達するまで単調増加するという特徴があります。(詳しくは「線形計算の数理」の4.3 Krylov部分空間を参照)
これに加え、固有値問題を解くアルゴリズムの一つであるべき乗法ではKrylov列のベクトルを正規化したものが\(A\)の固有ベクトルに収束することを利用していることからわかる通り、Krylov部分空間は\(A\)の固有ベクトル(特に絶対値が最大となる固有値の固有ベクトル)の成分を多く持つような空間を生成することができます。
べき乗法についてはこちらで詳しく紹介していますので、参考にしてみてください。
この二つの特性からKrylov部分空間を利用することでArnoldi法は\(A\)の固有値、固有ベクトルを\(A\)の次元よりもはるかに小さい行列を利用して計算することが可能となります。
また、Krylov列からグラムシュミットの正規直交化法によって正規直交基底\(\boldsymbol{v}_{1}, … \boldsymbol{v}_{m}\)を並べた行列\(V=[\boldsymbol{v}_{1}, … \boldsymbol{v}_{m}]\)とします。このとき、
$$ \begin{align*}
H = V^HAV
\tag{4.50}
\end{align*} $$
という風に作った\(H\)は\(m \times m\)のHessenberg行列で,上三角行列に下1行を追加した形の行列になることが知られています。Arnoldi法のアルゴリズムでは式(4.50)計算を直接やらずに、Krylov列のグラムシュミットの正規直交化を計算しながら\(H\)の生成も同時にやっています。ちなみに、この\(H\)と\(V\)を求める部分のアルゴリズムを本ではArnoldi算法という名前で紹介しています。
この\(H\)はHessenberg行列であるため、行列の対角成分の2つ以下が0になっています。このため、QR法なで固有値を求める際、QR分解で0の部分をスキップするなど高速化が可能となり、固有値を求めるには都合の良い行列になっています。
QR法についてはこちらの記事で紹介していますので、参考にしてみてください。
Pythonによる実装
ここからは紹介したアルゴリズムをPythonで実装したものを説明します。
実装は以下の通りです。
import numpy as np
def arnoldi_method(a, x0, m):
if m > a.shape[0]:
raise ValueError
n = a.shape[0]
h = np.zeros((m, m))
v = np.zeros((n, m))
v0 = x0 / np.linalg.norm(x0)
v[:, 0] = v0
k = 0
for k in range(m):
k = k
w = a @ v[:, k]
for j in range(k+1):
v_j = v[:, j]
h[j,k] = v_j.T @ w
w = w - h[j,k]*v_j
if k+1 < m:
h[k+1, k] = np.linalg.norm(w)
v[:, k+1] = w/h[k+1, k]
ritz_values, ritz_vectors = np.linalg.eig(h)
eigenvectors = v @ ritz_vectors
return ritz_values, eigenvectorsこれを以下のように実行して絶対値最大となる固有値とその固有ベクトル、そのときの残差のノルムを出力してみます。
import numpy as np
np.random.seed(1)
a_matrix = np.random.rand(8, 8)
n = a_matrix.shape[0]
x0 = np.ones(n)
eigenvalues, eigenvectors = arnoldi_method(a_matrix, x0, 4)
orders = np.argsort(-np.abs(eigenvalues))
print("eigenvalue:", eigenvalues[orders[0]])
print("eigenvector:")
print(eigenvectors[:, orders[0]])
r = a_matrix @ eigenvectors[:, orders[0]] - eigenvalues[orders[0]] * eigenvectors[:, orders[0]]
norm_r = np.linalg.norm(r)
print("||r||:", norm_r)この出力は以下のようになります。
eigenvalue: (3.4995258474334907+0j) eigenvector: [0.2046176 +0.j 0.38710413+0.j 0.42003848+0.j 0.32821558+0.j 0.48492918+0.j 0.38776328+0.j 0.18715778+0.j 0.32183775+0.j] ||r||: 0.004572773990371693
また、\(m\)を変化させると近似固有値、近似固有ベクトルの近似精度が良くなるのでそれも見てみます。以下のように\(m\)を変化させながら、絶対値が最大となる固有値の残差ノルムをプロットすると以下のようになります。
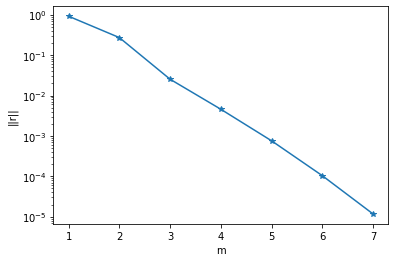
このように\(m\)が大きくなるにつれて残差が0に近づいていくことがわかります。
終わりに
今回はArnoldi法について紹介しました。今回のArnoldi法は読んだだけではわからないことが多く、実際に実装していろいろ値を変えてみてわかることが多かった印象があります。このため、実装まで作ってよかったと考えています。

