[勉強ノート] 「拡散モデル データ生成技術の数理」 2.3 デノイジング拡散確率モデル
先日紹介した「拡散モデル データ生成技術の数理」をちゃんと理解するために数式を改めて追ったり、説明されているアルゴリズムを実装したりしています。
その第3弾として「2.3 デノイジング拡散確率モデル」で説明されているデノイジング拡散確率モデル(DDPM)の学習とそれを使ったサンプリングについてPython(深層学習部分はPytorch)でコードを書いて試したのでそのまとめになります。今回の記事ではDDPMの細かい数式を説明すると記事の量がすごいことになりそうなので、重要な部分だけ説明していきます。
また、この本を買うか迷っている方は私が読んだ感想をこちらの記事に書いてますので参考にしてみてください。
また、この記事で紹介したコードは以下にあげてありますので、コード全体を確認したい方はこちらをご覧ください。
https://github.com/shu65/diffusion-model-book/blob/main/diffusion_model_book_2_3_ddpm.ipynb
デノイジング拡散確率モデルとは
デノイジング拡散確率モデル(DDPM)はデータに対して徐々にノイズを加えていく拡散過程を逆向きに辿っていく逆拡散過程によってデータ生成を行います。図でみると分かりやすいと思うので拡散過程と逆拡散過程の関係図を以下に示します。
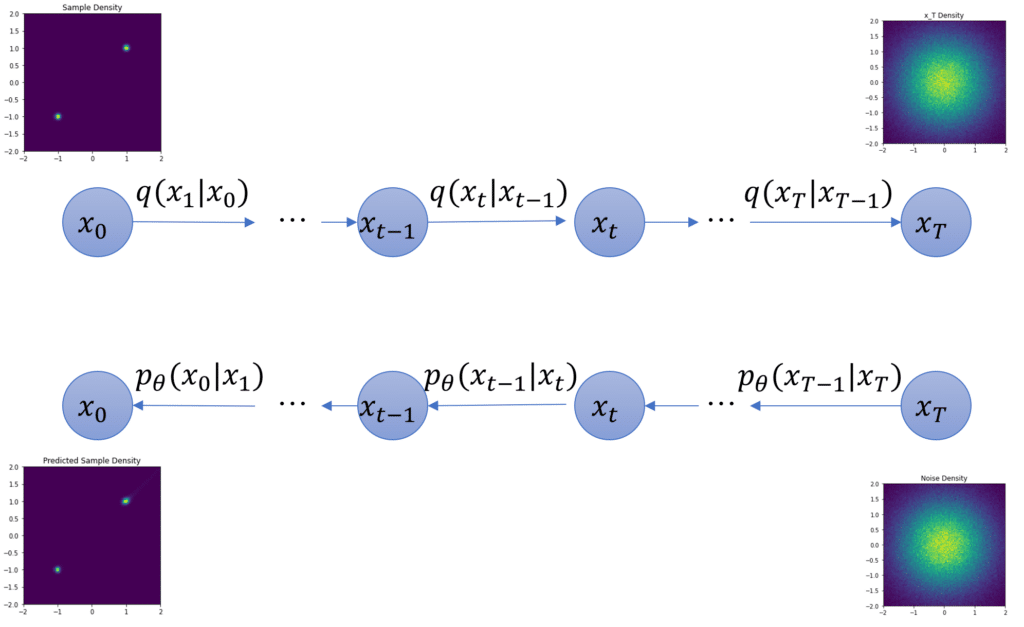
まずは上の図の上段の拡散過程についてです。ここでは\(\boldsymbol{x}_0\)がオリジナルのデータで、これに徐々にノイズを加えていき、\(\boldsymbol{x}_1, \boldsymbol{x}_2, \boldsymbol{x}_3, …, \boldsymbol{x}_T\)といいうデータを作っていきます。これを確率密度関数で表すと以下のようになります。
$$ \begin{align*}
q(\boldsymbol{x}_{1:T}|\boldsymbol{x}_0) :=& \prod_{t=1}^T q(\boldsymbol{x}_t|\boldsymbol{x}_{t-1}) \tag{2.1.1} \\
q(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1}) :=& \mathcal{N}(\boldsymbol{x}_t; \sqrt{\alpha_t}\boldsymbol{x}_{t-1}, \beta_t \boldsymbol{I}) \tag{2.1.2} \\
\end{align*} $$
ここで\(\beta_t\) は分散の大きさを制御するパラメータで、\(0<\beta_1<\beta_2<…<\beta_T<1\)です。また、\(\alpha_t := 1 – \beta_t\) で、\(\alpha_t, \beta_t\)を合わせてノイズスケジュールと呼びます。
ここで、\(\mathcal{N}(\boldsymbol{x}_t; \sqrt{\alpha_t}\boldsymbol{x}_{t-1}, \beta_t \boldsymbol{I})\) について詳しく見ていきます。この拡散過程を繰り返していくと、\(\beta_t\) は徐々に大きくなります。結果として、ノイズ成分は大きくなっていきます。
一方、\(\beta_t\)が大きくなるということは\(\alpha_t := 1 – \beta_t\) なので\(\boldsymbol{x}_{t-1}\)の係数の\(\sqrt{\alpha_t}\)はどんどん小さくなっていきます。結果として、拡散過程を繰り返していくと任意の\(\boldsymbol{x}_{0}\)に対して、以下のような近似ができるようになります。
$$ \begin{align*}
q(\boldsymbol{x}_{T}|\boldsymbol{x}_{0}) :=& \mathcal{N}(\boldsymbol{x}_T; 0, \boldsymbol{I}) \tag{2.1.3} \\
\end{align*} $$
次に、図の下段の逆拡散過程です。これは\(\mathcal{N}(\boldsymbol{x}_T; 0, \boldsymbol{I}) \)からスタートして拡散過程を逆向きに辿っていく処理になります。
この逆拡散過程の各ステップを正規分布で表し、この正規分布の平均と共分散行列を一つ前のステップの変数\(\boldsymbol{x}_{t}\)と時刻\(t\)を入力としてパラメータ\(\theta\)を使ったモデル(\(\mu_{\theta}(\boldsymbol{x}_{t}, t), \Sigma(\boldsymbol{x}_{t}, t))\))として表します。これを使うと逆拡散過程は以下のような式で表すことができます。
$$ \begin{align*}
p_{\theta}(\boldsymbol{x}_{0:T}) :=& p(\boldsymbol{x}_T)\prod_{t=1}^T p_{\theta}(\boldsymbol{x}_t-1|\boldsymbol{x}_{t}) \tag{2.1.4} \\
p_{\theta}(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t}) :=& \mathcal{N}(\boldsymbol{x}_{t-1}; \mu_{\theta}(\boldsymbol{x}_{t}, t), \Sigma_{\theta}(\boldsymbol{x}_{t}, t)) \tag{2.1.5} \\
p(\boldsymbol{x}_{T}) =& \mathcal{N}(\boldsymbol{x}_T; 0, \boldsymbol{I}) \tag{2.1.6}
\end{align*} $$
この\(\mu_{\theta}(\boldsymbol{x}_{t}, t), \Sigma_{\theta}(\boldsymbol{x}_{t}, t)\)は後ほど示す通りニューラルネットワークなどを使ってモデル化します。これによって逆拡散過程を実現しています。
では次から実際にこのモデルのパラメータ\(\theta\)の学習方法とそれを使ったサンプリングを見ていきます。
デノイジング拡散確率モデルの学習
デノイジング拡散確率モデルのモデルの学習方法の説明を本来はしたいのですが、この説明はすごく長いものになります。このため、詳しい説明は本を見ていただくとして、ここでは学習を回すうえで重要な変数と式に関する簡単な説明にとどめておきます。
まず、先ほど示した式(2.1.2)などを利用すると以下の式が導けます。
$$ \begin{align*}
q(\boldsymbol{x}_{t}|\boldsymbol{x}_{0}) :=& \mathcal{N}(\boldsymbol{x}_t; \sqrt{\bar{\alpha}_t}\boldsymbol{x}_{0}, \bar{\beta}_t \boldsymbol{I}) \tag{2.1.7} \\
\bar{\alpha}_t := \prod_{s=1}^t \alpha_s \tag{2.1.8} \\
\bar{\beta}_t := 1 – \bar{\alpha}_t \tag{2.1.9} \\
\end{align*} $$
式(2.1.7)から式(2.1.9)の導出の証明に関しては本の式(2.1)の下に証明がありますので詳しく知りたい方はそちらをご覧ください。
これにより、わざわざ式(2.1.2)に従って、\(\boldsymbol{x}_{0}\)から徐々に\(t\)を大きくして\(\boldsymbol{x}_{t}\)を生成しなくても、式(2.1.7)を使うことで正規分布のサンプリングを1度すれば任意の\(t\)の\(\boldsymbol{x}_{t}\)のデータを生成できることになります。学習ではこれを利用して高速にランダムな\(t\)のデータを生成して学習に利用します。
次にデノイジング拡散確率モデルの学習で用いるロス関数についてです。これに関しては前の記事でも紹介したスコアベースモデルと同じようにデノイジングスコアマッチングを利用します。また、ロス関数の導出は先ほど説明した通り、ちゃんと説明しようとするとすごく長いので本で示されている最終的な結果を以下に示します。
$$ \begin{align*}
L_{\gamma}(\theta) =& \sum_{t=1}^T w_t E_{\boldsymbol{x}_0, \epsilon} \left\{ \left\| \epsilon – \epsilon_{\theta}(\sqrt{\bar{\alpha}_t}\boldsymbol{x}_0 + \sqrt{\bar{\beta}_t}\epsilon, t) \right\|^2 \right\} \tag{2.1.10} \\
\gamma =& \left\{ w_1, w_2, …, w_T \right\} \tag{2.1.11}
\end{align*} $$
この式の\(w_t\)に関しては本によると\(w_t = 1\) がよくつかわれるとのことなので、このあとの実装のコードでも\(w_t = 1\)としています。
ここで、式の導出を省略して関係が分かりにくくなっていため、逆拡散過程の説明で出てきた式(2.1.5)の中の\(\mu_{\theta}(\boldsymbol{x}_{t}, t), \Sigma_{\theta}(\boldsymbol{x}_{t}, t)\)と式(2.1.10)の中で出てきている\(\epsilon_{\theta}(\sqrt{\bar{\alpha}_t}\boldsymbol{x}_0 + \sqrt{\bar{\beta}_t}\epsilon, t)\) との関係を説明しておきます。
逆拡散過程を行う上で\(\mu_{\theta}(\boldsymbol{x}_{t}, t), \Sigma_{\theta}(\boldsymbol{x}_{t}, t)\)のパラメータ\(\theta\)を学習する必要があります。ここで、本の説明によると\(\Sigma_{\theta}(\boldsymbol{x}_{t}, t)\)に関してはパラメータ\(\theta\)に依存しない固定の\(\Sigma_{\theta}(\boldsymbol{x}_{t}, t)) = \sigma_t^2 \boldsymbol{I}\)を使うことが多いそうです。先ほど示したロス関数も\(\Sigma_{\theta}(\boldsymbol{x}_{t}, t)) = \sigma_t^2 \boldsymbol{I}\)として式変形しています。
次に\(\mu_{\theta}(\boldsymbol{x}_{t}, t)\)の部分です。こちらはロス関数の導出の過程で結局は\(t\)の時点で加えられたノイズを予測できるモデルに置き換えることができます。このため、\(\mu_{\theta}(\boldsymbol{x}_{t}, t)\)ではなく、ノイズを予測する\(\epsilon_{\theta}(\boldsymbol{x}_{t}, t)\)がロス関数の中で登場しています。
また、\(\boldsymbol{x}_{t}\) は式(2.1.7)から以下のようになります。
$$ \begin{align*}
\boldsymbol{x}_{t} =& \sqrt{\bar{\alpha}_t}\boldsymbol{x}_0 + \sqrt{\bar{\beta}_t}\epsilon \\
\epsilon \sim& \mathcal{N}(0, \boldsymbol{I}) \\
\tag{2.1.12}
\end{align*} $$
本のほうには丁寧にこのロス関数の導出が書かれているので詳細を知りたい方はぜひ本を読んでください。
この式(2.1.10)をロス関数として利用したデノイジング拡散確率モデルの学習の疑似コードは以下の通りです。(「拡散モデル データ生成技術の数理」Algorithm 2.2の引用)
- repeat
- \(\quad \boldsymbol{x}_0 \sim p_{\text{data}}(\boldsymbol{x}_0)\)
- \(\quad t \sim \text{Uniform}({1, …, T})\)
- \(\quad \epsilon \sim \mathcal{N}(0, \boldsymbol{I})\)
- \(\quad g := \nabla_{\theta} w_t \left\| \epsilon – \epsilon_{\theta}(\sqrt{\bar{\alpha_t}} \boldsymbol{x}_0 + \sqrt{\bar{\beta_{t}}} \epsilon, t)\right\|^2 \)
- \(\quad \theta := \theta – \alpha g \)
- until converged
ここで本では特に説明されてないですが、式(2.1.10)の最初の\(\sum_{t=1}^T\)の部分は少し変更して、\(t=1\)から\(t=T\)ランダムに\(t\)を選んで使用するように変更されています。
このアルゴリズムでは、まず最初にデータ\(\boldsymbol{x}_0 \)と\(t\)を選び、それらを用いて式(2.1.10)のロス関数を計算します。その後、勾配を計算してパラメータのアップデートをするということを繰り返します。6行目の勾配を使ったパラメータのアップデートは深層学習の基本的なパラメータ更新の確率的勾配降下法を利用したコードになっています。この部分は確率的勾配降下法以外のもの、例えばAdamなどでも問題ありません。
この疑似コードを基にPyTorchで実装するとこのようになります。
batch_size = 512
n_steps = 100000
dataloader = torch.utils.data.DataLoader(dataset, batch_size=512, shuffle=True, num_workers=0)
dataloader_iter = iter(dataloader)
model = Model().to(device)
optimizer = torch.optim.Adam(model.parameters())
lr_scheduler = torch.optim.lr_scheduler.OneCycleLR(optimizer, max_lr=0.001, total_steps=n_steps)
loss_func = torch.nn.MSELoss(reduction="none")
for i in range(n_steps):
try:
x0 = next(dataloader_iter)[0]
except StopIteration:
dataloader_iter = iter(dataloader)
x0 = next(dataloader_iter)[0]
x0 = x0.to(device)
optimizer.zero_grad()
noise = torch.randn_like(x0)
t = torch.randint(0, len(x0), (x0.shape[0],), device=device)
x = torch.sqrt(alpha_bars[t])[:, None] * x0 + torch.sqrt(beta_bars[t])[:, None] * noise
noise_pred = model(x, t)
w = 1.0
losses = w * loss_func(noise_pred, noise)
loss = losses.mean()
loss.backward()
optimizer.step()
lr_scheduler.step()基本的には疑似コードとほぼ同じですが、ロス関数周りで違うところがあるので、簡単に説明します。まず、深層学習なのでミニバッチを使った学習に置き換えています。このため、\(\boldsymbol{x}_0 \)も一つだけでなく、バッチサイズ分ランダムに選んでいます。これに伴って、\(t\)もバッチサイズ分ランダムに選んで利用します。そして、最終的には各データ点のロス関数の値の平均を計算して勾配を計算するという形に置き換えています。
また、パラメータの最適化の部分は確率勾配降下法ではなくAdamを利用しています。
デノイジング拡散確率モデルを使ったサンプリング
ここから先ほど紹介した方法で学習したモデルを利用してどのようにサンプリングしていくか、について説明します。
基本的には式(2.1.5)に従って逆拡散過程のステップを繰り返すことで実現します。
ここで、説明を省略してしまいましたが、式(2.1.5)の中にでてくる\(\mu_{\theta}(\boldsymbol{x}_{t}, t)\)を学習したノイズを予測するモデル\(\epsilon_{\theta}(\boldsymbol{x}_{t}, t)\)を使って表すと以下のようになります。
$$ \begin{align*}
\mu_{\theta}(\boldsymbol{x}_{t}, t) =& \frac{1}{\sqrt{\bar{\alpha}}} \left( \boldsymbol{x}_{t} – \frac{\beta_t}{\sqrt{\bar{\beta_t}}} \epsilon_{\theta}(\boldsymbol{x}_{t}, t) \right) \tag{2.1.13}
\end{align*} $$
また、一方、\(\Sigma_{\theta}(\boldsymbol{x}_{t}, t))\)は先ほど説明した通り、\(\Sigma_{\theta}(\boldsymbol{x}_{t}, t)) = \sigma_t^2 \boldsymbol{I}\)です。
これらと式(2.1.5)に従ったサンプリングの疑似コードは以下の通りです。(「拡散モデル データ生成技術の数理」Algorithm 2.3の引用)
- \(\boldsymbol{x}_T \sim \mathcal{N}(0, \boldsymbol{I})\)
- for \(t=T, …, 1\) do
- \(\quad \boldsymbol{u}_t \sim \mathcal{N}(0, \boldsymbol{I})\)
- \(\quad\) if \(t=1\) then \(\boldsymbol{u}_t := 0\)
- \(\quad \boldsymbol{x}_{t-1} := \frac{1}{\sqrt{\bar{\alpha}}} \left\{ \boldsymbol{x}_{t} – \frac{\beta_t}{\sqrt{\bar{\beta_t}}} \epsilon_{\theta}(\boldsymbol{x}_{t}, t) \right\} + \sigma_t \boldsymbol{u}_t \)
- end for
- return \(\boldsymbol{x}_0\)
基本的には徐々にノイズを取り除くことで目的のデータをサンプリングするという流れです。
PyTorchのコードとしては以下のようになります。
def ddpm_sample(n_samples, model, alphas, betas, beta_bars):
xt = torch.randn(n_samples, 2)
T = len(alphas)
for t in range(T -1, -1, -1):
print(f"t:{t}")
ut = torch.randn(n_samples, 2)
if t == 0:
ut[:, :] = 0.0
with torch.no_grad():
noise_pred = model(xt, t*torch.ones(n_samples, dtype=xt.dtype))
sigma_t = torch.sqrt(betas[t])
xt = 1 / torch.sqrt(alphas[t]) * (xt - betas[t]/torch.sqrt(beta_bars[t])*noise_pred) + sigma_t*ut
return xtここで、n_samplesがサンプリングするサンプル数、modelが\(\epsilon_{\theta}(\boldsymbol{x}_{t}, t)\)、alphas、betas, beta_barsがそれぞれ\(\alpha_t, \beta_t, \bar{\beta}_t\) のリストです。
実行例
先ほど紹介したPythonコードを実際に動かした例も示しておきます。参考例として入力となる\(\boldsymbol{x}\)のサンプリングする分布の確率密度関数は以下のように平均が違うガウス分布二つの混合分布とし、サンプリングしたデータを正規化して使用します。
n_samples = int(1e6)
sigma = 0.01
dist0 = torch.distributions.MultivariateNormal(torch.tensor([-2, -2], dtype=torch.float).to(device), sigma*torch.eye(2, dtype=torch.float).to(device))
samples0 = dist0.sample(torch.Size([n_samples//2]))
dist1 = torch.distributions.MultivariateNormal(torch.tensor([2, 2], dtype=torch.float).to(device), sigma*torch.eye(2, dtype=torch.float).to(device))
samples1 = dist1.sample(torch.Size([n_samples//2]))
samples = torch.vstack((samples0, samples1))
mean = torch.mean(samples, dim=0)
std = torch.std(samples, dim=0)
normalized_samples = (samples - mean[None, :])/std[None, :]使用する\(\boldsymbol{x}\)を2Dのヒストグラムで可視化すると以下のようになります。
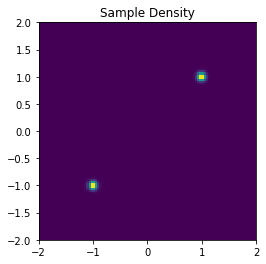
このデータを再現できるようにデノイジング拡散確率モデルを学習します。コードとしては先ほど示した通りです。
学習が終わったら次は以下のようにサンプリングを行います。
samples_pred = ddpm_sample(n_samples=100000, model=model, alphas=alphas, betas=betas, beta_bars=beta_bars)サンプリングされたデータの2Dのヒストグラムは以下の通りです。
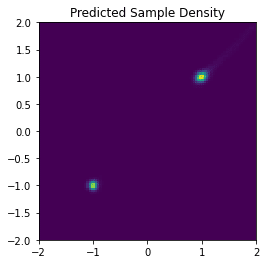
可視化結果をみると元の分布の平均の近くにデータが集中しているので、うまくいっていると考えられます。
終わりに
今回は「拡散モデル データ生成技術の数理」の2.3のデノイジング拡散確率モデルの簡単な説明とコードを書いたのでそのまとめの記事になります。先日スコアベースモデルのコードを用意したことで、そのコードを参考に今回のデノイジング拡散確率モデルをすぐに作ることができたのですが、説明はすごい大変でした。
スコアベースモデルのほうも気になるという方はこちらをご覧ください。
今後、3章で紹介されている連続時間化拡散モデルのVE-SDEのほうも紹介予定です。コードは昨日できました。ただ、思ったよりも説明が大変そうなので、記事を書くのに時間がかかると思います。
この記事が少しでもみなさんの理解の助けになれば幸いです。
参考文献
- Ho, J., Jain, A., & Abbeel, P. (2020). Denoising Diffusion Probabilistic Models. ArXiv, abs/2006.11239.
- https://github.com/hojonathanho/diffusion


