[勉強ノート]「ベイズ推論による機械学習入門」5.7 ニューラルネットワークで紹介されたものをPyTorchで実装してみた
目次
はじめに
最近ベイズ推論の勉強をしていて機械学習スタートアップシリーズの「ベイズ推論による機械学習入門」を読んでいます。今回はこの本の5.7 のニューラルネットワークの章で紹介されていたモデルをPyTorchで実装したので、実装と苦労した点を紹介していきます。
参考にしたJuliaのサンプルコードはこちらです。
https://github.com/sammy-suyama/BayesBook/blob/master/src/demo_BayesNeuralNet.jl
今回はこのサンプルコードをもとにして、PyTorchで実装したものを作り、以下に公開しました。
今回はこのPyTorch実装についての紹介になります。パラメータは少しいじっていますが大体Juliaのサンプルと合わせています。
PyTorchで実装することで、より複雑なモデルを作ることが簡単になるのと、単純作業だけどやるのは大変な偏微分の計算のところをPyTorchの自動微分に任せることができるため、より本質的なことろが理解しやすくなると思ったためです。
それではまず本に書かれているモデルについて簡単に説明して、その後実際のPyTorch実装の説明という流れで説明していきたいと思います。
本で紹介されているモデルと変分推論
モデルの定義
まずは本で紹介されているモデルについて説明していきます。訓練データの入力値と出力値の集合をそれぞれ \( \boldsymbol{X} \)、 \( \boldsymbol{Y} \) と置きます。この集合の要素数を \( N \) とし \( n \in N \) 番目のデータの入力値を \( \boldsymbol{x}_n \in \mathbb{R}^M \) 、出力値を \( \boldsymbol{y}_n \in \mathbb{R}^D \) とするとき、ガウス分布によってモデル化すると以下のようになります。
$$ \begin{align*}
p(\boldsymbol{Y}|\boldsymbol{X}, \boldsymbol{W})
=& \prod_{n=1}^N p(\boldsymbol{y}_n|\boldsymbol{x}_n, \boldsymbol{W}) \\
=& \prod_{n=1}^N \mathcal{N}(\boldsymbol{y}_n|f(\boldsymbol{W}, \boldsymbol{x}_n), \lambda_y^{-1}\boldsymbol{I}_D) \tag{5.257}
\end{align*} $$
ここで、\( \boldsymbol{W} \) は モデルのパラメータの集合、\( \lambda_y^{-1} \) 固定の精度パラメータです。また、非線形関数\(f\)は次のように定義することにします。
$$ \begin{align*}
f(\boldsymbol{W}, \boldsymbol{x}_n) = {\boldsymbol{W}^{(2)}}^\mathrm{T} \text{Tanh}({\boldsymbol{W}^{(1)}}^\mathrm{T}\boldsymbol{x}_n) \tag{5.258}
\end{align*} $$
ここでモデルパラメータ \( \boldsymbol{W} \) の要素を\( \boldsymbol{W}^{(1)} \) と \( \boldsymbol{W}^{(2)} \)として、\( \boldsymbol{W}^{(1)} \in \mathbb{R}^{M \times K}\) 及び\( \boldsymbol{W}^{(2)} \in \mathbb{R}^{K \times D}\) という行列としています。このモデルパラメータの各要素は次のようなシンプルなガウス事前分布を仮定することにします。
$$ \begin{align*}
p (w_{m,k}^{(1)}) = \mathcal{N} (w_{m,k}^{(1)}|0, \lambda_w^{-1}) \tag{5.259} \\
p (w_{m,k}^{(2)}) = \mathcal{N} (w_{m,k}^{(2)}|0, \lambda_w^{-1}) \tag{5.259}
\end{align*} $$
また \( \text{Tanh}(\cdot) \) は以下のように定義されます。
$$
\text{Tanh}(a) = \frac{\text{exp}(a) – \text{exp}(-a)}{\text{exp}(a) + \text{exp}(-a)} \tag{5.261}
$$
以上が本に書かれたモデルの定義になります。
変分推論
ここではニューラルネットワークモデルのパラメータ \( \boldsymbol{W} = \{ \boldsymbol{W}^{(1)}, \boldsymbol{W}^{(2)} \} \) の事後分布を推論する問題を考えます。こちらは本で一つ前に紹介されていたロジスティック回帰のときとほぼ同じように行っていきます。
今回は細かい式の説明は省いていますが、ニューラルネットワークの勾配の計算は5.6ロジスティック回帰と似たような式変形になります。5.6ロジスティック回帰の式の導出はこちらの記事に詳しく書いてあるので参考にしてみてください。
事後分布を推定するために、対角ガウス分布を使った以下のような近似事後分布を利用します。
$$ \begin{align*}
q(\boldsymbol{W}^{(1)}; \boldsymbol{\eta}^{(1)}) =& \prod_{m=1}^M \prod_{k=1}^K \mathcal{N}(w_{m,k}|\mu_{m,k}^{(1)},{\sigma_{m,k}^{(1)}}^2) \tag{5.262.1} \\
q(\boldsymbol{W}^{(2)}; \boldsymbol{\eta}^{(2)}) =& \prod_{m=1}^M \prod_{k=1}^K \mathcal{N}(w_{m,k}|\mu_{m,k}^{(2)},{\sigma_{m,k}^{(2)}}^2) \tag{5.262.2} \\
\end{align*} $$
ここで \( \boldsymbol{\eta} = \{ \boldsymbol{\eta}^{(1)}, \boldsymbol{\eta}^{(2)} \} \) が変分パラメータの集合となります。今回は以下のような近似事後分布と真の事後分布のKLダイバージェンスを最小化するような変分パラメータ \( \boldsymbol{\eta} \)を見つけることを目指します。
$$ \begin{align*}
&\text{KL} [q(\boldsymbol{W};\boldsymbol{\eta})||p(\boldsymbol{W}|\boldsymbol{Y},\boldsymbol{X})] \\
& \ = \langle \ln q(\boldsymbol{W};\boldsymbol{\eta}) \rangle _{q(\boldsymbol{W};\boldsymbol{\eta})}
– \langle \ln p(\boldsymbol{W}) \rangle _{q(\boldsymbol{W};\boldsymbol{\eta})} \\
& \qquad – \sum_{n=1}^N \langle \ln p(\boldsymbol{y}_n | \boldsymbol{x}_n, \boldsymbol{W}) \rangle _{q(\boldsymbol{W};\boldsymbol{\eta})}
+ \text{const} \tag{5.236}
\end{align*} $$
この式 (5.236)の最小化するにあたり、以下のような再パラメータ化トリックを利用して、 \( \boldsymbol{W} \) の各要素 \( w \) (インデックスは省略してます。) を以下のように置きます。
$$ \begin{align*}
\tilde{w} = \mu + \sigma \tilde{\epsilon} \tag{5.237} \\
\text{ただし} \tilde{\epsilon} \sim \mathcal{N} (\epsilon|0,1) \tag{5.238}
\end{align*} $$
これを利用すると以下のような \( g(\boldsymbol{\tilde{W}}, \boldsymbol{\eta}) \) を最小化することになります。
$$ \begin{align*}
& \text{KL} [q(\boldsymbol{W};\boldsymbol{\eta})||p(\boldsymbol{W}|\boldsymbol{Y},\boldsymbol{X})] \\
& \ \approx \ln q(\boldsymbol{\tilde{W}};\boldsymbol{\eta})
– \ln p(\boldsymbol{\tilde{W}}) \\
& \qquad – \sum_{n=1}^N \ln p(\boldsymbol{y}_n | \boldsymbol{x}_n, \boldsymbol{\tilde{W}}) + \text{const} \\
& \ = g(\boldsymbol{\tilde{W}}, \boldsymbol{\eta}) \tag{5.239}
\end{align*} $$
ただし、本ではすべてのデータで尤度の勾配を計算する方法ではなく、確率的勾配降下法(stochastic gradient descent, SGD)にも触れられているので、この記事ではSGDを使って最適化します。ただ、後ほどまた説明しますが、本で書かれているデータを1つ1つ逐次的に与えて勾配を計算するオンラインのSGDではうまく収束してくれなかったので、ミニバッチを用いるSGDを使います。これは基本的に本で書かれているように式(5.239) の事前分布と近似事後分布の項の影響をデータ数に応じて抑えます。今回はミニバッチを利用するので、ミニバッチ内の訓練データを\( \{\boldsymbol{X}_B, \boldsymbol{Y}_B\}\)とし、 \( b \in B \) 番目のデータの入力値を \( \boldsymbol{x}_b\) 、出力値を \( \boldsymbol{y}_b \)として式 (5.239) を変形した以下の式の勾配を利用します。
$$ \begin{align*}
& \text{KL} [q(\boldsymbol{W};\boldsymbol{\eta})||p(\boldsymbol{W}|\boldsymbol{Y}_B,\boldsymbol{X}_B)] \\
& \ \approx \frac{B}{N} \lbrace \ln q(\boldsymbol{\tilde{W}};\boldsymbol{\eta})
– \ln p(\boldsymbol{\tilde{W}}) \rbrace \\
& \qquad – \sum_{b=1}^B \ln p(\boldsymbol{y}_b | \boldsymbol{x}_b, \boldsymbol{\tilde{W}}) + \text{const} \\
\tag{5.269.1}
\end{align*} $$
本ではこれ以外に勾配を計算するための式変形が細かく書いてありますが、今回はPyTorchの自動微分の機能を使うため、式 (5.269.1) の値を計算し、この値をlossとしてbackward() を実行するため、説明はここまでにします。
実装について
今回はPyTorchの自動微分の機能を使って変分パラメータの最適化に必要な勾配を計算します。このため、処理の基本的な流れとしては式 (5.269.1) の値を計算し、この値をlossとしてbackward() を実行するというのを指定した回数繰り返して最適化します。
モデル部分の実装
式 (5.258) をPyTorchで実装します。具体的なものは最初に示したJupyter Notebookの BayeNNModel クラスの実装をご覧ください。ここでは重要な部分だけ示します。まず、式 (5.258)を forward() に実装します。
def forward(self, X):
W1 = self.sample_W(self.mu1, self.rho1)
h1 = torch.nn.functional.linear(X, W1, bias=None)
h2 = torch.tanh(h1)
W2 = self.sample_W(self.mu2, self.rho2)
Y_est = torch.nn.functional.linear(h2, W2, bias=None)
return Y_est, W1, W2今回は \( \boldsymbol{\tilde{W}} \) はサンプリングしてくる必要があるので、sample_W() という関数でサンプリングしてそれをtorch.nn.functional.linear()に入れるということをしています。
\( \boldsymbol{\tilde{W}} \) はサンプリングしてくる部分は以下のようにします。
def sample_W(self, mu, rho):
eps = torch.randn(mu.shape)
sigma = self.rho2sigma(rho) + self.approximate_posterior_sigma_eps
W = mu + sigma * eps
return W基本的には式(5.237) の実装になります。ただ、後ほど説明する \( \ln q(\boldsymbol{\tilde{W}};\boldsymbol{\eta}) \) の計算のところで、ガウス分布に入れる \( \sigma \) が0になってしまいエラーになるケースが発生してしまうため、0にならないようにするための補正 (self.approximate_posterior_sigma_eps) を加算しています。
変分推論部分の実装
勾配を計算するための式(5.269.1) の各項を計算します。これらの項はすべてガウス分布になっているのでPyTorchの torch.distributions.normal.Normal() を使えば簡単に実装できます。
\( \ln q(\boldsymbol{\tilde{W}};\boldsymbol{\eta}) \) と\( \ln p(\boldsymbol{\tilde{W}}) \) 、\( \sum_{b=1}^B \ln p(\boldsymbol{y}_b | \boldsymbol{x}_b, \boldsymbol{\tilde{W}}) \)のそれぞれの項は以下の関数で計算するようにしています。
def _compute_approximate_posterior_log_prob_core(self, W, mu, rho):
sigma = self.rho2sigma(rho) + self.approximate_posterior_sigma_eps
W_dist = torch.distributions.normal.Normal(mu, sigma)
log_prob_W = W_dist.log_prob(W)
sum_log_prob_W = torch.sum(log_prob_W)
return sum_log_prob_W
def _compute_prior_log_prob_core(self, W, sigma_w):
W_dist = torch.distributions.normal.Normal(0, sigma_w)
log_prob_W = W_dist.log_prob(W)
sum_log_prob_W = torch.sum(log_prob_W)
return sum_log_prob_W
def compute_approximate_posterior_log_prob(self, W1, W2):
log_prob_W1 = self._compute_approximate_posterior_log_prob_core(W1, self.mu1, self.rho1)
log_prob_W2 = self._compute_approximate_posterior_log_prob_core(W2, self.mu2, self.rho2)
return log_prob_W1 + log_prob_W2
def compute_prior_log_prob(self, W1, W2):
log_prob_W1 = self._compute_prior_log_prob_core(W1, self.sigma_w)
log_prob_W2 = self._compute_prior_log_prob_core(W2, self.sigma_w)
return log_prob_W1 + log_prob_W2
def compute_log_prob_p(self, Y, Y_est):
Y_dist = torch.distributions.normal.Normal(Y_est, self.sigma_y)
log_p = Y_dist.log_prob(Y)
return torch.sum(log_p)これらを使ってKLダイバージェンスの勾配に関係する部分だけ計算して、backward()とOptimizerのstep()を以下のように呼びます。
def vi_step(X, Y, model, optimizer, N, max_grad_norm=1e2):
model.zero_grad()
batch_size = X.shape[0]
Y_est, W1, W2 = model(X)
prior_log_prob_W = model.compute_prior_log_prob(W1, W2)
posterior_log_prob_W = model.compute_approximate_posterior_log_prob(W1, W2)
log_prob_p = model.compute_log_prob_p(Y, Y_est)
kl_divergence = batch_size/N * (posterior_log_prob_W - prior_log_prob_W) - log_prob_p
kl_divergence.backward()
torch.nn.utils.clip_grad_norm_(model.parameters(), max_grad_norm)
optimizer.step()
return kl_divergence.item()これらを使ってJuliaのサンプルと同様の訓練データで事後分布の推定を行って本の図5.18と似たような図を以下のように作ってみました。
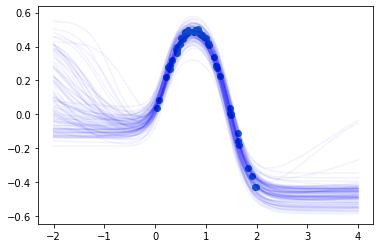
図を見ると十分な精度がでていると思っています。
実装で苦労した点について
いざ実装してみると以下の点で工夫が必要だったので簡単に紹介します。
最初の数イテレーションの勾配が大きすぎてモデルのパラメータがnanになる
最初の数イテレーションはどうしても勾配が大きくなりがちです。今回は特にバッチサイズが大きいとモデルのパラメータが途中でnanになってしまうという問題が発生しました。この手の問題は深層学習ではよくあるためいくつか対処する手段はありますが、今回はシンプルなgradient clippingを利用しています。具体的には vi_step() でtorch.nn.utils.clip_grad_norm_()を呼んでいる部分がそれにあたります。
近似事後分布のσが0になる
バッチサイズや他のパラメータによっても発生したりしなかったりしますが、時々\( \ln q(\boldsymbol{\tilde{W}};\boldsymbol{\eta}) \)を計算する部分で \( \sigma \) が計算誤差で0に丸められてしまうとうケースが発生しました。このため、以下のようにして小さい値を加算して0になるのを防ぐ必要がありました。
sigma = self.rho2sigma(rho) + self.approximate_posterior_sigma_eps
W_dist = torch.distributions.normal.Normal(mu, sigma)終わりに
「ベイズ推論による機械学習入門」の5.7 ニューラルネットワークのモデルをPyTorchで実装したので、実装についてと苦労した点についての記事を書きました。
実装する前はすぐできるだろうと思っていましたが、苦労した点に書いたような問題が出てきて思ったより時間がかかった印象です。ただ、実際に実装してみてベイズ推論の理解が深まったのでやってよかったです。実はこの本の他の実装もいつくかしてあるので機会があればまたblogの記事にしようと思います。

