[勉強ノート] 「拡散モデル　データ生成技術の数理」 1.5.1 ランジュバン・モンテカルロ法

最近、先日紹介した「拡散モデル　データ生成技術の数理」をちゃんと理解するために数式を改めて追ったり、説明されているアルゴリズムを実装したりしています。

今回はその第１弾として「1.5.1 ランジュバン・モンテカルロ法」の部分で紹介されているランジュバン・モンテカルロ法を実装をして動かすとどうなるのか？を試してみたので、そのまとめの記事になります。

今回示しているコードはここに上がっています。

https://github.com/shu65/diffusion-model-book/blob/main/diffusion_model_book_1_5_1_langevin_monte_carlo.ipynb

また、この本を買うか迷っている方はこちらの記事に私が読んだ感想を書いてますので参考にしてみてください。

ランジュバン・モンテカルロ法とは？

ランジュバン・モンテカルロ法は拡散モデルで登場するMCMC法の１つであり、 \(p(\boldsymbol{x})\)のスコアと呼ばれるものが計算できれば\(p(\boldsymbol{x})\)からサンプリングしたものに近い\(\boldsymbol{x}\)が得られる手法です。

ランジュバン・モンテカルロ法は拡散モデルを学習後、生成のフェーズにおいて使われるので拡散モデルを理解するうえでランジュバン・モンテカルロ法は重要な手法です。

このランジュバン・モンテカルロ法の疑似コードは以下の通りです。(「拡散モデル　データ生成技術の数理」Algorithm 1.1の引用)

1. \(\boldsymbol{x}_0\)を初期化(\(\boldsymbol{x}_0 \sim \mathcal{N}(0, \boldsymbol{I})\))
2. for \(k=1,…,K\) do
3. \(\quad \boldsymbol{u}_k\ \sim \mathcal{N}(0, \boldsymbol{I})\)
4. \(\quad \boldsymbol{x}_k\ := \boldsymbol{x}_{k-1} + \alpha \nabla_{\boldsymbol{x}}\log p(\boldsymbol{x}_{k-1}) + \sqrt{2 \alpha}\boldsymbol{u}_k\)
5. end for
6. return \(\boldsymbol{x}_K\)

ここで、\(\alpha\)はステップ幅、\(K\)はステップ回数、\(p(\boldsymbol{x})\)が\(\boldsymbol{x}\)の確率密度関数です。また、\(\nabla_{\boldsymbol{x}}\log p(\boldsymbol{x}) \)が\(\boldsymbol{x}\)に対するスコアです。

疑似コードを見ていただければわかる通り、最初、ランダムに\(\boldsymbol{x}_0\)を生成後、以下のランジュバン・モンテカルロ法の更新則を\(K\)回繰り返すことで\(p(\boldsymbol{x})\)からサンプリングしたようなデータを作ります。

$$ \begin{align*}
\boldsymbol{x}_k := \boldsymbol{x}_{k-1} + \alpha \nabla_\boldsymbol{x} \log p(\boldsymbol{x}_{k-1}) + \sqrt{2\alpha}\boldsymbol{u}_k \\
\end{align*} $$

Pythonでランジュバン・モンテカルロ法を実装する

ここからPythonでランジュバン・モンテカルロ法を実装して実際に動かした様子を見ていきます。

まずは実装に関してです。ここではスコア(\(\nabla_{\boldsymbol{x}}\log p(\boldsymbol{x}) \))を簡単に計算するために深層学習ライブラリのPyTorchを利用します。PyTorchには自動微分の機能がありこれにより\(\nabla\)が簡単に計算することができます。

先ほど示したアルゴリズムをそのままPyTorchで実装すると以下のようになります。

def langevin_monte_carlo_algorithm(log_p_dist, n_samples=100000, alpha=0.001, K=1000):
    x0 = torch.randn(n_samples, 2)
    x_k = x0
    for i in tqdm(range(K+1)):
        x_k.requires_grad_()
        log_p = log_p_dist(x_k)
        score = torch.autograd.grad(log_p.sum(), x_k)[0]
        with torch.no_grad():
          u_k = torch.randn(n_samples, 2)
          x_k = x_k + alpha * score + np.sqrt(2 * alpha) * u_k
    return x_k

ここでlog_p_distはサンプリングしたい分布の確率密度関数の出力を対数にしたものを返す関数です。後ほど具体例を示しますが、PyTorchで\(\nabla\)を計算したいのでlog_p_distは自動微分が計算できるPyTorchの関数だけで計算する関数である必要があります。

また、x_kは自動微分により\(\nabla\)を計算する必要があるのでx_k.requires_grad_()として、torch.autograd.grad()を呼んだときが自動微分の結果が入るようにしておきます。これに加えて実際に自動微分を計算する際にPyTorchの制約上、torch.autograd.grad()のoutputs（ここではlog_p.sum()のところ）がスカラである必要があります。このため、そのままlog_pをtorch.autograd.grad()に引数で渡すとエラーになってしまうため、log_p.sum()をでスカラにしてからtorch.autograd.grad()の引数にいれています。

Pythonで実装したランジュバン・モンテカルロ法

次に先ほど示した実装を動かしてみます。ここでサンプリングする分布の確率密度関数は以下のように平均が違うガウス分布二つの混合分布としました。

def log_p_dist(x):
  dist0 = torch.distributions.MultivariateNormal(torch.tensor([-2, -2]), torch.eye(2))
  p0 = torch.exp(dist0.log_prob(x))
  dist1 = torch.distributions.MultivariateNormal(torch.tensor([2, 2]), torch.eye(2))
  p1 = torch.exp(dist1.log_prob(x))
  return torch.log((p0 + p1)/2.0)

確率密度関数を可視化してみると以下のようになります。

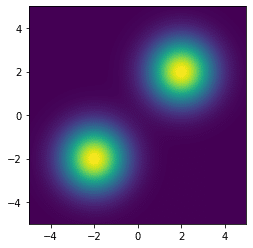
次にランジュバン・モンテカルロ法を使ってサンプリングしてみます。実行方法としては以下の通りです。

samples_1em1 = langevin_monte_carlo_algorithm(log_p_dist, alpha=1e-1)

これでヒストグラムを描くと以下のようになります。

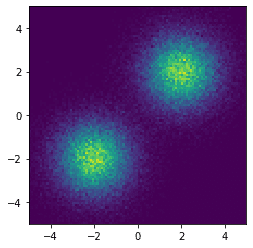
図を見ていただければわかる通り、確率密度関数に近いヒストグラムを得ることができていることがわかります。

ここまでできたので、折角なので２章あたりで指摘される問題点の１つである\(\alpha\)の値の設定によってうまくサンプリングできない例を確認してみます。

具体的には\(\alpha\)を以下のように極端に小さくして実行してみます。

samples_1em5 = langevin_monte_carlo_algorithm(log_p_dist, alpha=1e-5)

ヒストグラムを描くとこのようになります。

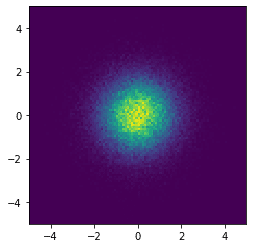
\(\alpha\)の値を変な値にすると入力した確率密度関数とは全く違う分布になってしまうことがわかりました。これで２章の説明の重要性を実感することができました。

終わり

今回はランジュバン・モンテカルロ法の解説とPythonの実装を示しました。今回の章は比較的簡単に実装できました。ただ、このあと紹介する予定の部分は説明を聞くと簡単そうですが、実装するのは大変な部分が多い印象です。ですが、頑張って紹介できればと思っています。