[勉強ノート] 入門 統計的因果推論 反事実における直接効果と間接効果、媒介公式の導出 (4.5.2 媒介についてのツール)

今回の記事は入門 統計的因果推論 の4.5.2に書かれている「反事実における直接効果と間接効果の定義」、「自然な効果を識別するための条件」を中心にここで説明されている直接効果、間接効果の定義からdo演算子を使わない媒介公式などの式の導出について説明していきます。

この部分も私はぱっと読んで意味がわからなくて苦労した点なので、自分であとで見返してもわかるように丁寧な説明を心がけて書いていこうと思います。

想定する因果グラフ

この記事で想定している因果グラフは以下の通りです。

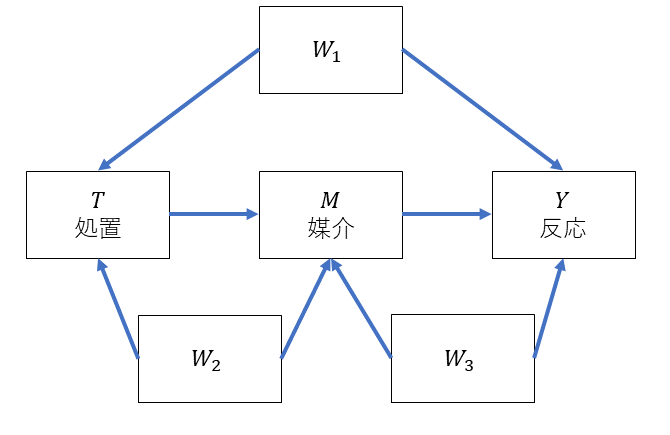
本では媒介公式の式導出の部分（自然な効果を識別するための条件の節）で\(W\)として抽象的な変数を使ってまとめています。この記事でも基本同様に\(W\)でまとめていますが、この因果グラフでは\(W_1, W_2, W_3\)と具体的にして分けています。

直接効果と間接効果の定義

まずはこれらの定義がどういうものかを見ていきます。本に書かれている定義は以下の通りです。

総合効果TE (total effect)

$$ \begin{align*}
TE &= E[Y_1 – Y_0] \\
&=E[Y|do(T=1) – E[Y|do(T=0)]]\tag{4.44}
\end{align*} $$

ここで\(Y_x\)は本ででてくる表記で\(X=x\)の場合の\(Y\)を\(Y_x\)ということを表しています。具体的には本の4.1の「反事実」の例で下道を使った場合とフリーウェイを使った場合の運転時間の例で説明します。このとき、フリーフェイを使うケースを\(T=1\)とするとこの時の運転時間\(Y\)を\(Y_{T=1}\)、\(T\)が自明な時は\(Y_1\)ということを表しています。一方、下道を使った場合\(T=0\)の運転時間は\(Y_{T=0}\)または\(Y_0\)です。

このTEは処置\(T=0\)から\(T=1\)へ変化したときの\(Y\)の増加量です。重要な点として媒介変数\(M\)は\(T\)が変化するにつれて変化します。

制御された直接効果CDE (controlled direct effect)

$$ \begin{align*}
CDE(m) &= E[Y_{1,m} – Y_{0,m}] \\
&=E[Y|do(T=1, M=m)] – E[Y|do(T=0, M=m)]\tag{4.45}
\end{align*} $$

\(Y_{1,m}\)の部分は省略されていますが、\(Y_{T=1, M=m}\)の意味です。基本的には統合効果のときに説明したときとほぼ同じで、ここでは\(T\)だけでなく\(M\)についても固定した状態の\(Y\)の値を示しています。

このCDEは処置\(T=0\)から\(T=1\)への変化したときのYの増加量の期待値ですが、重要な点として媒介変数\(M\)は\(M=m\)で一律に設定されています。

自然な直接効果NDE (natural direct effect)

$$ \begin{align*}
NDE &= E[Y_{1,M_0} – Y_{0,M_0}] \tag{4.46}
\end{align*} $$

このNDEは処置が\(T=0\)から\(T=1\)へ変化したときの\(Y\)の増加量の期待値ですが、重要な点として媒介変数は変化前の状態、つまりT=0においてそれぞれの個体がとったであろう値(\(M_0\))に固定されています。この\(M_0\)は\(M_{T=0}\)を表していて、\(M\)が\(T=0\)のときの値を示しています。この媒介変数の値が一律で固定されているケースがCDEで、変化前の状態で個別にとったであろう値に固定されているのがNDEになります。

自然な間接効果NIE (natural indirect effect)

$$ \begin{align*}
NIE &= E[Y_{0,M_1} – Y_{0,M_0}] \tag{4.47}
\end{align*} $$

このNIEでは処置が\(T=0\)で固定されているときのYの増加量の期待値です。このとき媒介変数\(M\)は\(T=1\)においてそれぞれの個体がとったであろう値に変化させます。よって、\(Y\)が\(T\)で反応しないようにしたうえで媒介変数によって変化する量を表しています。

NDEとNIEを識別する十分条件 (自然な効果を識別するための条件)

先ほどのNDEとNIEまで計算するための十分条件として本には以下のように書かれています。

1. \(W\) の要素(最初の因果グラフでは\(W_1, W_2, W_3\))には\(T\)の子孫が一つもない
2. \(W\) は(\(T\rightarrow M\)と\(T\rightarrow Y\)を除いた)\(M\)から\(Y\)へのバックドアパスをすべてブロックする
3. \(T\)から\(M\)への特定\(W\)同時効果は(おそらく実験か調整により)識別可能である
4. \(\{T, M\}\)から\(Y\)への特定\(W\)同時効果は(おそらく実験か調整により)識別可能である

ここで\(W\)は因果グラフにおける\(\{W_1, W_2, W_3\}\)をまとめた変数になります。

これらの条件は言葉で言わんとしていることはわかるきがしますが、これを使って私はNDEとNIEの媒介公式を導出できるきがしませんでした。このため、別の表現がないかな？ということで探すと、別の論文[1]に別の表現の条件が書かれていたので今回はこの条件を使って証明していきます。

まず、一致性 (consistency assumption) と構成性 (composition assumption)という以下の仮定が成り立つとします。

• 一致性: \(T=t\)と\(M=m\)が条件付けされたとき\(Y=Y_{t, m}\)が成り立つ。同様に\(T=t\)が条件付けされたとき\(M=M_t\)が成り立つ
• 構成性: \(T=t\)が条件付けされたとき\(Y(t) = Y_{t, M(t)}\)が成り立つ

そしてNDEとNIEが識別可能とする十分条件として以下のものがあるとしています。

$$ \begin{align*}
Y_{t, m} & \perp\kern-5pt\perp T \mid W & \forall t, m \tag{A-1} \\
Y_{t, m} & \perp\kern-5pt\perp M \mid T, W & \forall t, m \tag{A-2} \\
M_t & \perp\kern-5pt\perp T \mid W & \forall t \tag{A-3} \\
Y_{t, m} & \perp\kern-5pt\perp M_{t^{\star}} \mid W & \forall t, t^{\star}, m \tag{A-4} \\
\end{align*} $$

変数に関しては今回の因果グラフに合わせて元論文から変更しています。

各効果の定義から式変形していく

ここから本では省略されている式変形をしていって、観測データから計算できる形に式を持っていきたいと思います。定義では期待値の形で書かれていますが、確率がわかれば十分だと思うので、確率の形で式変形していきます。TEに関しては３章で示されているdo演算子を使った場合の式変形を行えば目的の式まで変形できますが、他の効果の定義に合わせて先ほどの仮定と条件を使って式変形していきます。

ちなみに３章で示されているdo演算子を使った場合の式変形はこちらで詳しく書いていますので気になる方は見てください。

[勉強ノート] 入門 統計的因果推論 3章 介入効果　

TE

TEの定義は以下の通りです。

$$ \begin{align*}
TE &= E[Y_1 – Y_0] \\
&=E[Y|do(T=1)] – E[Y|do(T=0)]]\tag{4.44}
\end{align*} $$

ここで\(P(Y|do(X))\)からdo演算子のない形にするというのでもいいのですが、先ほどの仮定と条件を使うために\(Y_1, Y_0\)から式変形していきます。ここで\(Y_1, Y_0\)をまとめて\(Y_t\)として計算していきます。

最終的には以下のような式になることを示します。

$$ \begin{align*}
P(Y_t) &= \sum_w P(Y|T=t, W=w)P(W=w) \tag{4.44.1}
\end{align*} $$

まず、構成性から以下の式に変形できます。

$$ \begin{align*}
P(Y_t) &= P(Y_{t, M_t}) \tag{4.44.2}
\end{align*} $$

ここで、確率の周辺化で以下の式が成り立つことを利用します。

$$ \begin{align*}
P(Y) =& \sum_x P(Y, X=x) \tag{4.44.3} \\
\end{align*} $$

この周辺化の式を使って\(W\)と\(M_t\)の同時確率の式に変形します。そして、その後、\(W\)と\(M_t\)の条件つき確率の形にもっていきます。

$$ \begin{align*}
P(Y_t) =& P(Y_{t, M_t}) \\
=& \sum_w P(Y_{t, M_t}, W=w) \\
=& \sum_w \sum_m P(Y_{t, M_t}, M_t=m, W=w) \\
=& \sum_w \sum_m P(Y_{t, M_t}, M_t=m|W=w)P(W=w) \\
=& \sum_w \sum_m P(Y_{t, M_t}| M_t=m, W=w)\\
& \qquad P(M_t=m|W=w)P(W=w) \tag{4.44.4}
\end{align*} $$

ここで\(M_t=m\)を利用すると以下のように変形できます。

$$ \begin{align*}
P(Y_{t, M_t}| M_t=m, W=w) &= P(Y_{t, m}| M_t=m, W=w) \tag{4.44.5}
\end{align*} $$

次に十分条件の中のA-1を利用すると式(4.44.5)は\(T=t\)を使った条件付き確率に変形できます。

$$ \begin{align*}
P(Y_{t, m}| M_t=m, W=w) &= P(Y_{t, m}| M_t=m, T=t, W=w) \tag{4.44.6}
\end{align*} $$

そして一致性を使うと\(P(Y_{t, m}| M_t=m, W=w)\)は以下のようになります。

$$ \begin{align*}
P(Y_{t, m}| M_t=m, T=t, W=w) &= P(Y| M_t=m, T=t, W=w) \tag{4.44.7}
\end{align*} $$

よって式(4.44.5)から(4.44.7)を利用すると式(4.44.4)は以下のように変形できます。

$$ \begin{align*}
P(Y_t) =& \sum_w \sum_m P(Y_{t, M_t}| M_t=m, W=w) \\
& \qquad P(M_t=m|W=w)P(W=w) \\
=& \sum_w \sum_m P(Y_{t, m}| M_t=m, W=w) \\
& \qquad P(M_t=m|W=w)P(W=w) \\
=& \sum_w \sum_m P(Y_{t, m}| M_t=m, T=t, W=w)\\
& \qquad P(M_t=m|W=w)P(W=w) \\
=& \sum_w \sum_m P(Y| M_t=m, T=t, W=w)\\
& \qquad P(M_t=m|W=w)P(W=w) \tag{4.44.8}
\end{align*} $$

最後に\(M_t=m\)の条件付き確率を同時確率の形に戻して、周辺化を適用して\(M_t=m\)の部分を取り除くと以下のようになります。

$$ \begin{align*}
P(Y_t) =& \sum_w \sum_m P(Y| M_t=m, T=t, W=w)\\
& \qquad P(M_t=m|W=w)P(W=w) \\
=& \sum_w \sum_m P(Y, M_t=m| T=t, W=w)P(W=w) \\
=& \sum_w P(Y| T=t, W=w)P(W=w) \tag{4.44.9}
\end{align*} $$

これで求めたい式(4.44.1)が導出できました。

CDE

次にCDEについても式変形していきます。CDEの定義は以下の通りです。

$$ \begin{align*}
CDE(m) &= E[Y_{1,m} – Y_{0,m}] \\
&=E[Y|do(T=1, M=m)] – E[Y|do(T=0, M=m)]\tag{4.45}
\end{align*} $$

これをTEのときと同じようにdo演算子がない状態に\(Y_{1,m}\)と\(Y_{0,m}\)を式変形していきたいと思います。\(Y_{1,m}\)と\(Y_{0,m}\)をまとめて\(Y_{t,m}\)という形で式変形していきます。

CDEの場合は最終的に以下の式の導出を目指します。

$$ \begin{align*}
P(Y_{t,m}) &= \sum_w P(Y|M=m, T=t, W=w)P(W=w) \tag{4.45.1}
\end{align*} $$

それでは\(P(Y_{t,m})\)を周辺化の式を使って\(W\)の同時確率の形にして、その後\(W\)の条件付き確率の形にします。

$$ \begin{align*}
P(Y_{t,m}) &= \sum_w P(Y_{t,m}, W=w) \\
&= \sum_w P(Y_{t,m}|W=w)P(W=w)\tag{4.45.2}
\end{align*} $$

次に\(P(Y_{t,m}|W=w)\)に注目するとA-1の条件から\(W\)が与えられると\(Y_{t,m}\)と\(T\)は独立なため、\(P(Y_{t,m}|W=w)\)を\(T=t\)の条件付き確率にできます。

$$ \begin{align*}
P(Y_{t,m}|W=w) &= P(Y_{t,m}|T=t, W=w) \tag{4.45.3}
\end{align*} $$

さらにA-2の条件から\(W\)と\(T\)が与えられると\(Y_{t,m}\)と\(M\)は独立なため、\(P(Y_{t,m}|T=t, W=w)\)を\(M=m\)の条件付き確率にできます。

$$ \begin{align*}
P(Y_{t,m}|T=t, W=w) &= P(Y_{t,m}|M=m, T=t, W=w) \tag{4.45.4}
\end{align*} $$

ここで一致性から以下のように変形できます。

$$ \begin{align*}
P(Y_{t,m}|M=m, T=t, W=w) &= P(Y|M=m, T=t, W=w)\tag{4.45.5}
\end{align*} $$

最後に式(4.45.2)を式(4.45.3)から式(4.45.5)を利用して変形していきます。

$$ \begin{align*}
P(Y_{t,m}) &= \sum_w P(Y_{t,m}, W=w) \\
&= \sum_w P(Y_{t,m}|W=w)P(W=w) \\
&= \sum_w P(Y_{t,m}|T=t, W=w)P(W=w) \\
&= \sum_w P(Y_{t,m}|M=m, T=t, W=w)P(W=w) \\
&= \sum_w P(Y|M=m, T=t, W=w)P(W=w) \tag{4.45.6}
\end{align*} $$

以上でCDEのほうも導出することができました。

NDEとNIE

最後にNDEとNIEです。それぞれ以下のような定義になっています。

$$ \begin{align*}
NDE &= E[Y_{1,M_0} – Y_{0,M_0}] \tag{4.46} \\
NIE &= E[Y_{0,M_1} – Y_{0,M_0}] \tag{4.47} \\
\end{align*} $$

これは\(Y_{1,M_0}, Y_{0,M_0}, Y_{0,M_1}, Y_{0,M_0}\)の４種類の確率が分かればよいことがわかります。これらの変数をまとめて\(Y_{t_y,M_{t_m}}\)としてこの後まとめて式変形していきます。最終的には以下の式に変形することを目指します。

$$ \begin{align*}
P(Y_{t_y,M_{t_m}}) =& \sum_w \sum_m P(Y|M=m, T=t_y, W=w)\\
& \qquad P(M|T=t_m, W=w)P(W=w) \tag{4.46.1}
\end{align*} $$

まずは\(W\)の同時確率の形にして、その後\(W\)の条件付き確率の形に変形します。

$$ \begin{align*}
P(Y_{t_y,M_{t_m}}) &= \sum_w P(Y_{t_y,M_{t_m}}, W=w) \\
&= \sum_w P(Y_{t_y,M_{t_m}}|W=w)P(W=w) \tag{4.46.2}
\end{align*} $$

次に\(P(Y_{t_y,M_{t_m}}|W=w)\)の部分に注目して\(M_{t_m}\)に関しても同様に周辺確率の形にしてその後\(M_{t_m}\)の条件付き確率の形に変形します。

$$ \begin{align*}
P(Y_{t_y,M_{t_m}}|W=w) &= \sum_m P(Y_{t_y,M_{t_m}}, M_{t_m}=m|W) \\
&= \sum_m P(Y_{t_y,M_{t_m}}|M_{t_m}=m, W=w)P(M_{t_m}=m|W) \tag{4.46.3}
\end{align*} $$

ここで\(M_{t_m}=m\)を利用すると以下のように変形できます。

$$ \begin{align*}
P(Y_{t_y,M_{t_m}}|W=w) &= \sum_m P(Y_{t_y,M_{t_m}}|M_{t_m}=m, W=w)P(M_{t_m}=m|W) \\
&= \sum_m P(Y_{t_y,m}|M_{t_m}=m, W=w)P(M_{t_m}=m|W) \tag{4.46.4}
\end{align*} $$

ここから\(P(M_{t_m}|W)\)の部分の式変形をしていきます。十分条件のA-3から\(W\)が条件付けされたとき、\(M_t\)と\(T\)は独立なので以下が成り立ちます。

$$ \begin{align*}
P(M_{t_m}|W) &= P(M_{t_m}|T=t_m, W) \tag{4.46.5}
\end{align*} $$

そして一致性から以下のようになります。

$$ \begin{align*}
P(M_{t_m}|W) &= P(M_{t_m}|T=t_m, W) \\
&= P(M|T=t_m, W) \tag{4.46.6}
\end{align*} $$

次に式(4.46.4)の\(P(Y_{t_y,m}|M_{t_m}=m, W)\)も式変形していきます。十分条件のA-4を利用すると\(W\)が条件付けされたとき、\(Y_{t_y,m}\)と\(M_{t_m}\)は独立なので以下のようになります。

$$ \begin{align*}
P(Y_{t_y,m}|M_{t_m}=m, W) &= P(Y_{t_y,m}|W) \tag{4.46.7}
\end{align*} $$

そして十分条件のA-1を使うと\(W\)が条件付けされたとき、\(Y_{t_y,m}\)と\(T\)は独立なので以下のようになります。

$$ \begin{align*}
P(Y_{t_y,m}|W=w) &= P(Y_{t_y,m}|T=t_y, W) \tag{4.46.8}
\end{align*} $$

同様に十分条件のA-2を使うと\(T\)と\(W\)が条件付けされたとき、\(Y_{t_y,m}\)と\(M\)は独立なので以下のようになります。

$$ \begin{align*}
P(Y_{t_y,m}|T=t_y, W) &= P(Y_{t_y,m}|M=m, T=t_y, W)\tag{4.46.9}
\end{align*} $$

ここで一致性から以下のようになります。

$$ \begin{align*}
P(Y_{t_y,m}|M=m, T=t_y, W) &= P(Y|M=m, T=t_y, W) \tag{4.46.10}
\end{align*} $$

式(4.46.7)から(4.46.10)までを利用すると最終的に以下のような関係が成り立ちます。

$$ \begin{align*}
P(Y_{t_y,m}|M_{t_m}=m, W) &= P(Y|M=m, T=t_y, W) \tag{4.46.11}
\end{align*} $$

式(4.46.6)と式(4.46.11)を使うと式(4.46.4)は以下のようになります。

$$ \begin{align*}
P(Y_{t_y,M_{t_m}}|W=w) =& \sum_m P(Y_{t_y,M_{t_m}}|M_{t_m}=m, W=w)\\
& \qquad P(M_{t_m}=m|W) \\
=& \sum_m P(Y_{t_y,m}|M_{t_m}=m, W=w)\\
& \qquad P(M|T=t_m, W) \\
=& \sum_m P(Y|M=m, T=t_y, W)\\
& \qquad P(M|T=t_m, W) \tag{4.46.12}
\end{align*} $$

最終的に式(4.46.12)を使うと式(4.46.2)は以下のようになります。

$$ \begin{align*}
P(Y_{t_y,M_{t_m}}) =& \sum_w P(Y_{t_y,M_{t_m}}, W=w) \\
=& \sum_w P(Y_{t_y,M_{t_m}}|W=w)P(W=w) \\
=& \sum_w \sum_m P(Y|M=m, T=t_y, W=w)\\
& \qquad P(M|T=t_m, W=w)P(W=w) \tag{4.46.13}
\end{align*} $$

これで求めたい式(4.46.1)の導出ができました。

終わりに

今回の記事は入門 統計的因果推論 の4.5.2に書かれているTE, CDE, NDE, NIEについて式変形をしていきました。一度理解してblogにかけそうと思ってからいざ書き始めたら、blogの記事を書く中でところどころ自分の理解が甘い部分が発見できました。このためblogの記事を書くことで自分の理解の再確認ができて非常に有意義でした。

他にもわからない部分がいくつかまだあるので、機会があれば勉強のために記事にしていきたいと思います。

参考文献

1. VanderWeele, Tyler J. and Stijn Vansteelandt. “Conceptual issues concerning mediation, interventions and composition.” Statistics and Its Interface 2 (2009): 457-468.